RoutingTables

Updating Routing Tables

(Proposed algorithm by Ryan)

When new edges are added or deleted, mark incident nodes as dirty.

Updating process:

Make a temporary copy of each dirty node's old routing table. Update each dirty node's routing table in the following fashion:
1. For each new edge, set the distance to the new neighbour to 1.
2. For each deleted edge, set the distance to the old neighbour to inf.
Mark each dirty node as seed.
For each seed node S, and each of its neighbours N, update N's routing table in the following fashion:
1. Store a temporary copy of N's soon-to-be old routing table.
2. (Propagating new edges.) For every entry S[X] in S's routing table, set the corresponding entry N[X] in N's routing table to N[X] = min(S[X] + 1, N[X])
3. (Propagating deleted edges.) For every entry N[Y] != inf such that S[Y] == inf, look at S'[Y], the distance from S to Y in S's old routing table. If S'[Y] == N[Y] - 1, set N[Y] = min(M[Y]) for all neighbours M of N. (This could be an expensive step.)
4. If N's routing table is changed, mark N as seed. Otherwise, delete the temporary copy of N's old routing table.
Delete the temporary copy of S's old routing table.
Repeat step 3 until no more seed nodes remain.

Does not require loading all tables into memory simultaneously.

Jevgenij: some interesting observations here. It's easy to locate nodes whose routing table entries will be affected: the condition is abs(d1 - d2) > 1. The PostgreSQL query (looking more tricky than it actually is - a query on a <join of two queries> - I hope it can be made more elegant) for that is something like:

SELECT * FROM (SELECT * FROM (SELECT dest_node_id, distance as d1 FROM routing_table WHERE src_node_id = <ID1>) AS leftpart JOIN (SELECT dest_node_id,distance AS d2 from routing_table WHERE src_node_id=<ID2>) AS rightpart USING (dest_node_id)) AS nodes_n_dists WHERE abs(d1 - d2) > 1

Alternative algorithm

Recompute from scratch. The problem is that usual methods require loading all routing tables into memory simultaneously.

Jevgenij: Could you explain here: why does it require all the routing tables to be in memory? - I don't see serious reasons for that. Did you mean the whole adjacency list? Or, would you prefer to have no topology representation other than routing tables at all?

Network representations

The obvious way to represent the network is to give each user one or more nodes, where each node connects accounts that it exchanges between:

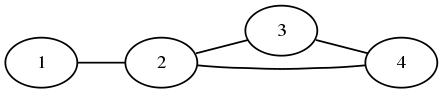
The problem with this is that it does not allow a natural representation of one-way exchanges. One-way exchanges are not expected to be the norm, but ought to be allowed, for example, when someone wants to convert from a foreign currency to their local one, but not back.

To represent the directionality of exchanges that a user can perform, exchanges must become the edges of the new graph, and then accounts, which are the edges of the old graph, become the nodes of the new graph:

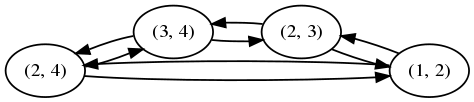
Here we have labelled accounts by the two users they connected in the original graph.

This seems OK at first, and it also gives a natural way to specify payments to a particular account. But what it does not specify is which account partner will receive the payment. What if user 1 wants to pay user 2, and user 2 wants to receive payment on her account with user 3, labelled (2,3)?

From the graph we currently have, it looks like we could just take path (1,2) -> (2,3). But we see from the original graph that that makes no sense, since it is asking user 2 to receive payment on her account with user 1, and then call that equivalent to her account with 3, since she has declared an exchange rate between the two. But what she really wants is to hold obligations from user 3 instead of from user 1, and our current graph is misleading.

What we really need to do is turn account (2,3) into two separate nodes, one where user 2 receives payment, and one where user 3 receives payment. We will call the one where user 2 receives payment (3,2), and the one where user 3 receives payment (2,3). Now the graph looks like:

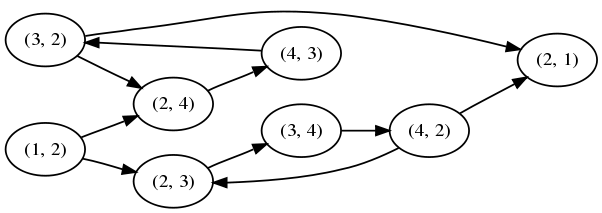
Now each path in the graph represents a real payment that we can actually make.

Well, that's not quite true: Because each account between users is represented by two separate nodes in our routing graph, it's possible that a path in the routing graph crosses back over the same underlying account in the opposite direction without making a loop in the routing graph. So we have to watch for this. Going back through the same user is OK, because it might be the only way to make the required exchanges, or to get to the target account -- so long as we don't cross back over the same account.